Cách tính thể tính hình hộp chữ nhật chính xác và dễ nhớ

Thể tích hình hộp chữ nhật là một trong những dạng toán cơ bản, phổ biến cả trong học tập và thực tế. Vậy nên, trong nội dung bài viết ngay sau đây sẽ tổng hợp đầy đủ thông tin từ công thức, cách tính và bài tập liên quan tới thể tích của hình hộp chữ nhật để mọi người có thể theo dõi và áp dụng.

Hình hộp chữ nhật là gì?

Hình hộp chữ nhật là một dạng hình học không gian với 6 mặt đều là hình chữ nhật. Trong đó, có 2 mặt không có cạnh chung gọi là 2 mặt đối diện hay là mặt đáy, còn các mặt còn lại gọi là mặt bên.

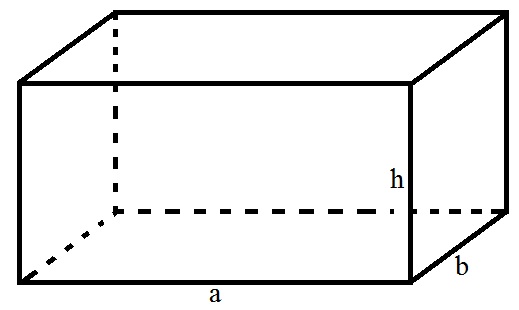
Hình hộp chữ nhật là một hình học không gian đặc biệt. (Ảnh: Sưu tầm internet)

Một số tính chất của hình hộp chữ nhật:

Hình chữ nhật có 12 cạnh, 8 đỉnh và 6 mặt.
Các đường chéo có 2 đầu mút là 2 đỉnh đối nhau của hình hộp chữ nhật đồng quy tại 1 điểm
Diện tích của 2 mặt đối diện trong hình hộp chữ nhật bằng nhau
Chu vi của 2 mặt đối diện trong hình hộp chữ nhật bằng nhau

Công thức tính thể tích hình hộp chữ nhật

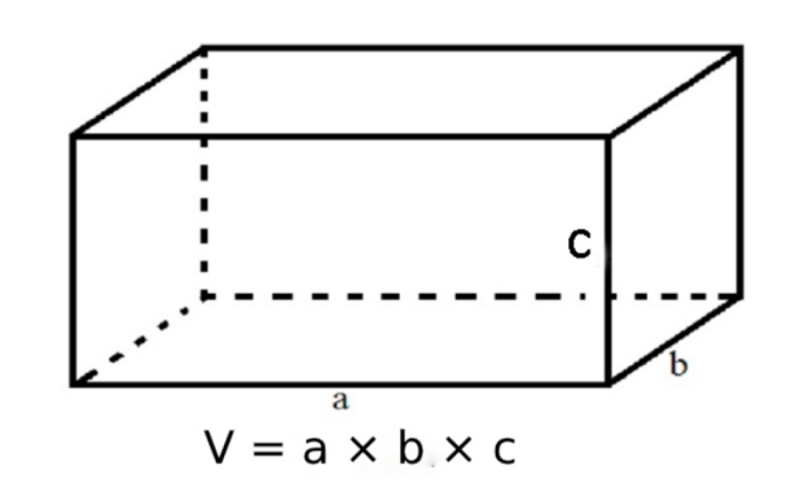
Công thức tính thể tích hình hộp chữ nhật là nhân chiều dài của mặt đáy (dài) với chiều rộng của mặt đáy (rộng), sau đó nhân với chiều cao của khối hộp.

Công thức tổng quát là: Thể tích (V) = Chiều dài (dài) * chiều rộng (rộng) * chiều cao (cao), hay V = drc = a*b*c. Trong đó:

V: thể tích hình hộp chữ nhật.
a: chiều dài hình hộp chữ nhật.
b: chiều rộng hình hộp chữ nhật.
h: chiều cao hình hộp chữ nhật.

Công thức tính thể tích của hình hộp chữ nhật. (Ảnh: Sưu tầm internet)

Một số cách tính thể tích hình hộp chữ nhật khác

Ngoài cách tính theo công thức tổng quát, bạn có thể tính thể tích hình hộp chữ nhật bằng các cách sau:

Cách 1: Cách tính tổng diện tích của ba mặt bên và cạnh bằng nhau

Công thức này là: V = 2(ab + ac + bc), trong đó a và b lần lượt là chiều dài và chiều rộng, c là chiều cao.

Ví dụ:

Cho một hộp chữ nhật có chiều dài a = 5 cm, chiều rộng b = 3 cm và chiều cao c = 4 cm.

Ta có thể tính thể tích bằng cách tính tổng diện tích các mặt bên và cạnh bằng nhau.

S = 2(a*b + a*4 + b*c) = 2(5*3 + 5*4 + 3*4) = 94 cm^3

Cách 2: Cách tính thể tích khi biết diện tích mặt đáy của hình hộp chữ nhật

Nếu diện tích mặt đáy (Sd) của hình hộp chữ nhật đã biết, bạn có thể tính được một trong hai thông số còn lại như a hoặc b (chiều dài hoặc chiều rộng). Với chiều dài và chiều rộng là hai kích thước của mặt đáy, ta có công thức Sd = a*b. Dựa trên công thức này, ta có thể tính toán và tìm ra thông số bị thiếu.

Sau khi bạn đã xác định được tất cả các thông số cần thiết, hãy sử dụng công thức V = a*b*c (nếu bạn đã biết a, b và c) để tính toán thể tích của khối hộp chữ nhật.

Cách 3: Công thức tính thể tích khi biết chu vi khối chữ nhật

Nếu chu vi (C) của hình hộp chữ nhật đã biết, bạn cần biết ít nhất hai trong ba thông số còn lại (a, b và c). Chu vi C được tính bằng công thức: C = 4a + 4b + 4c.

Các dạng bài tập về cách tính thể tích hình hộp chữ nhật và phương pháp giải

Đối với chuyên đề tính thể tích của khối hộp chữ nhật, các em sẽ được làm quen với một số dạng bài tập cơ bản sau đây:

Có nhiều dạng bài tập về tính thể tích hình hộp chữ nhật. (Ảnh: Sưu tầm internet)

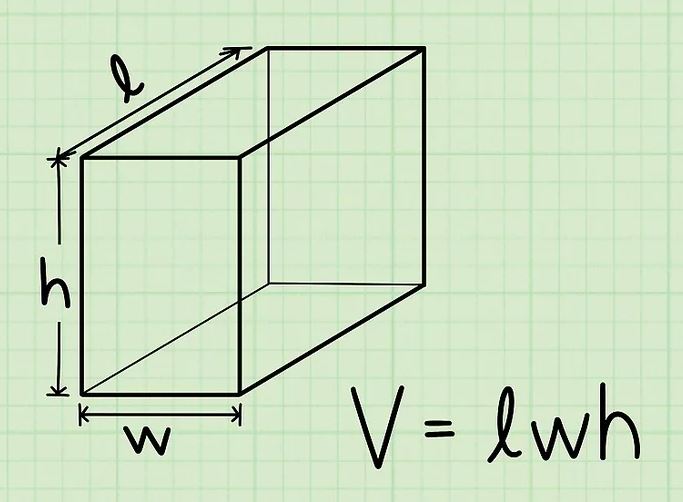
Dạng 1: Cách tính thể tích của một hộp chữ nhật khi biết chiều dài, chiều rộng và chiều cao.

Ví dụ: Cho hình hộp chữ nhật biết chiều dài 6cm, chiều rộng 3cm và chiều cao 2cm. Tính thể tích hình đó.

Hướng dẫn giải:

Thể tích hình hộp chữ nhật là:

V = l x w x h

V = 6cm x 3cm x 2cm

V = 36cm^3

Dạng 2: Cho hình hộp chữ nhật biết thể tích, hai kích thước tương ứng và yêu cầu tính kích thước cạnh còn lại.

Ví dụ: Tính chiều rộng của một hộp chữ nhật có thể tích 240cm^3, chiều dài 8cm và chiều cao 5cm.

V = l x w x h240cm^3 = 8cm x w x 5cmw = 6cm

Dạng 3: Tính chiều cao hình hộp chữ nhật khi biết 2 kích thước cạnh và thể tích tương ứng

Ví dụ: Cho hình hộp chữ nhật, biết thể tích 420cm^3, chiều dài 14cm và chiều rộng 3cm. Tính chiều cao của hình?

V = l x w x h420cm^3 = 14cm x 3cm x hh = 10cm

Dạng 4: Cách tính thể tích của một số hộp chữ nhật được cắt bỏ một phần.

Ví dụ: Cho hình hộp chữ nhật biết chiều dài 12cm, chiều rộng 6cm và chiều cao 3cm nếu một phần của hộp bị cắt bỏ. Thể tích hình là bao nhiêu?

V = l x w x hV = (12cm x 6cm x 3cm) - (4cm x 3cm x 3cm)V = 648cm^3 - 36cm^3V = 612cm^3

Dạng 5: Tính thể tích của một hộp chữ nhật khi có một lỗ hình tròn được đục ra khỏi một mặt phẳng của nó.

Ví dụ: Cho hình hộp chữ nhật với chiều dài 10cm, chiều rộng 8cm và chiều cao 6cm nếu một lỗ hình tròn bán kính 2cm được đục ra khỏi một mặt phẳng của nó. Thể tích hình là bao nhiêu?

V = l x w x hV = (10cm x 8cm x 6cm) - (pi x 2cm^2 x 6cm)V = 480cm^3 - 75.4cm^3V = 404.6cm^3

Dạng 6:. Cách tính thể tích của một hộp chữ nhật khi một góc của nó bị cắt bỏ.

Ví dụ: Cho hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 4cm nếu một góc của nó bị cắt bỏ. Thể tích hình là bao nhiêu?

V = l x w x hV = (8cm x 6cm x 4cm) - (2cm x 2cm x 4cm)V = 192cm^3 - 16cm^3V = 176cm^3

Dạng 7: Tính thể tích của một số hộp chữ nhật không đều, có các mặt phẳng lệch nhau.

Ví dụ: Cho hình hộp chữ nhật không đều, có chiều dài 10cm, chiều rộng 5cm và chiều cao 4cm. Mặt phẳng dưới cùng của hộp là một hình tam giác đều với cạnh 6cm. Tính thể tích của hình.

V = l x w x hV = (10cm x 5cm x 4cm) + (1/2 x 6cm x 4cm)V = 200cm^3 + 12cm^3V = 212cm^3

Xem thêm: Công thức tính thể tích hình lập phương & hướng dẫn giải chi tiết

Bài tập tính thể tích hình hộp chữ nhật cơ bản đến nâng cao

Dựa vào những kiến thức trên, dưới đây Monkey sẽ tổng hợp một số bài tập liên quan từ cơ bản đến nâng cao để các em có thể vận dụng và giải bài tập nhé!

Các bài tập về cách tính thể tích hình hộp chữ nhật cơ bản

Bài 1: Hình hộp chữ nhật có chiều dài 8 m, chiều rộng 5 m và chiều cao 6 m. Tính đường chéo của hình hộp chữ nhật.

Bài 2: Một hồ chứa nước có dạng hình hộp chữ nhật có thể tích là 3000 m3, chiều rộng là 10 m và chiều cao của hồ là 12 m. Tính chiều dài của hồ.

Bài 3: Cho hình hộp chữ nhật với chiều dài là 2,5cm, chiều rộng là 1,8 cm và chiều cao là 2cm. Hãy tính thể tích, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật đó đó.

Bài 4: Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích đáy SABCD = 24cm2 và có thể tích V = 84 cm3. Chiều cao của hình hộp chữ nhật có độ dài là?

Bài 5: Tính thể tích của khối hộp ABCD.A'B'C'D', biết rằng AA'B'D' là khối tứ diện đều cạnh a.

Bài 6: Một bể nước hình hộp chữ nhật có chiều dài 2m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước của bể là 0,8m.

a) Tính chiều rộng của bể nước.

b) Người ta đổ thêm vào bể 60 thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?

Các bài tập áp dụng công thức tính thể tích hình hộp chữ nhật nâng cao

Trong chương trình lớp 8 và lớp 12, các em sẽ được mở rộng kiến thức về mặt phẳng. Vì vậy, ngoài dạng bài tính thể tích hình hộp chữ nhật, các em sẽ được làm quen với các dạng toán xác định thể tích tối đa/ tối thiểu, so sánh thể tích 2 khối hộp & các bài toán ứng dụng thực tế.

Bài 1: Cho một hình hộp chữ nhật có các kích thước tỉ lệ với 3; 4; 5 và thể tích của hình hộp là 60cm3. Tính thể tích lớn nhất của khối hộp đó.

Bài 2: Hình lập phương A có cạnh bằng

$\frac{1}{2}$ cạnh hình lập phương B. Hỏi thể tích hình lập phương A bằng bao nhiêu phần thể tích hình lập phương B

Bài 3: Một bể cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài 1 m, chiều rộng 70 cm, chiều cao 60 cm. Mực nước trong bể cao 30 cm. Người ra cho vào bể một hòn đá thì thể tích tăng 14000 cm3. Hỏi mực nước trong bể lúc này cao bao nhiêu.

Đáp án bài tập tính thể tích hình hộp chữ nhật nâng cao

Bài 1:

Gọi kích thước của hình hộp chữ nhật đã cho là a, b, c

Vì các kích thước tỉ lệ với 3; 4; 5 nên:

$\frac{a}{3} = \frac{b}{4} = \frac{c}{5} = t$

Thể tích của hình hộp là:

V = abc nên: 3t. 4t. 5t= 480

Suy ra: 60t3 = 60 nên t = 1

Do đó, a = 3cm; b = 4cm; c = 5cm

Vậy cạnh lớn nhất của hình hộp là 5cm

Bài 2:

Gọi chiều dài một cạnh của hình lập phương A là a.

Vì hình lập phương A có cạnh bằng $\frac{1}{2}$ cạnh của hình lập phương B nên chiều dài 1 cạnh của hình lập phương B là 2a

Thể tích hình lập phương A là:

VA = a3.

Thể tích hình lập phương B là:

VB = (2a)3 = 8a3

=> VB = 8VA

=> VA = $\frac{1}{8}$ VB

Vậy thể tích hình lập phương A bằng $\frac{1}{8}$ thể tích hình lập phương B

Bài 3:

Đổi 1m = 100 cm

Thể tích phần bể chứa nước ban đầu là:

V = 100.70.30 = 210000 cm3

Sau khi cho vào một hòn đá thể tích tăng 14000 cm3. Vậy thể tích phần bể chứa nước lúc sau là:

V1 = V + 14000

= 210000 + 14000 = 224000 cm3

Vì chiều dài và chiều rộng bể nước không thay đổi nên sự thay đổi là do chiều cao mực nước thay đổi. Gọi chiều cao mực nước lúc sau là h cm. Ta có:

V = 100.70.h = 224000

=> h = = 32 cm

Bí quyết nắm vững cách tính thể tích V hình hộp chữ nhật

Để giúp các em học kiến thức này dễ hiểu, dễ áp dụng hơn khi giải toán hay ứng dụng trong thực tiễn thì dưới đây là một số kinh nghiệm để mọi người tham khảo:

Nắm chắc kiến thức cơ bản về hình hộp chữ nhật

Để giải được bài tập về tính thể tích hình hộp chữ nhật, đòi hỏi các em phải nắm chắc được những kiến thức liên quan tới hình học này, từ khái niệm, tính chất, đặc điểm, công thức tính và cách giải các dạng bài tập tương ứng….Ba mẹ nên dành thời gian để hướng dẫn bé học và kiểm tra lại bài cũ của con, để biết được bé đang gặp khó khăn ở phần nào, để từ đó củng cổ, giải thích để tránh tình trạng con “học trước quên sau”.

Luyện tập thực hành thường xuyên

Học đi đôi với hành là yếu tố bắt buộc nếu muốn hiểu rõ được kiến thức mình đã học. Vậy nên, ba mẹ nên khích lệ, yêu cầu bé nên thực hành, làm bài tập về tính thể tích khối hình hộp chữ nhật, hay bất kỳ bài tập nào thường xuyên hơn. Ngoài ra, có thể cho con tham gia các cuộc thi, tổ chức trò chơi, tham gia các hoạt động về toán học… Qua đó giúp kích thích khả năng tư duy và năng lực toán học của bé tốt hơn.

Việc thực hành, làm bài thật thường xuyên rất quan trọng. (Ảnh: Sưu tầm internet)

Tạo sự hứng thú khi học toán hình cùng Monkey Math

Monkey Math được biết đến là ứng dụng dạy học toán online dành cho trẻ mầm non và tiểu học, với nội dung được xây dựng bám sát chương trình GDPT mới nhất của Bộ đưa ra. Điều này góp phần giúp bé vừa phát triển năng lực học toán, vừa hỗ trợ việc học trên trường lớp đạt kết quả tốt hơn.

Điểm đặc biệt của Monkey Math chính là không dạy học theo phương pháp truyền thụ kiến thức thông thường, thay vào đó sẽ áp dụng những phương pháp dạy học tích cực như thông qua trò chơi, các hoạt động tương tác, đố vui, sách bài tập bổ trợ… Qua đó giúp bé dễ dàng có sự hứng thú và niềm yêu thích khi học toán hơn.

Đồng thời, nội dung bài học trên ứng dụng tổng hợp đa dạng chuyên đề từ đại số đến hình học, bao gồm cả chủ đề về hình hộp chữ nhật. Tất cả được phân chia thành nhiều cấp độ từ dễ đến khó, cá nhân hoá cho từng đối tượng để phụ huynh dễ dàng lựa chọn cấp độ phù hợp nhất với bé.

Đảm bảo mỗi giờ học toán cùng Monkey Math với bé là mỗi niềm vui, cũng như kích thích khả năng tư duy và năng lực toán học của trẻ phát triển hơn mỗi ngày. Để hiểu rõ hơn về ứng dụng, ba mẹ có thể tham khảo video sau, hoặc đăng ký để được tư vấn miễn phí nhé.

Trên đây là những thông tin giúp mọi người hiểu rõ hơn về cách tính thể tích hình hộp chữ nhật. Đây là kiến thức không chỉ áp dụng trong toán học mà trong thực tiễn ứng dụng rất nhiều, nên ba mẹ hãy tham khảo để có thêm thông tin hướng dẫn bé học tốt hơn. Đồng thời, nếu không có nhiều thời gian và kinh nghiệm trong việc dạy bé học toán thì có thể tham khảo ứng dụng Monkey Math nhé.